The Cross-Convex Bestiary
Collection of cross-convex functions (in magenta) with their tangent surface (in green): https://github.com/mastane/TheXCB
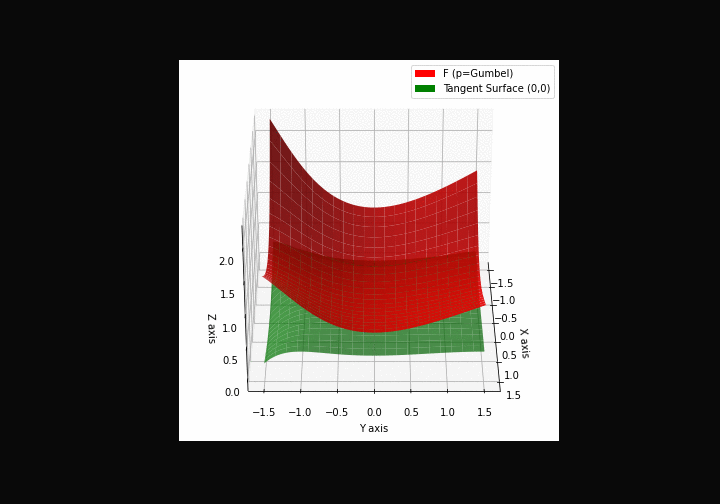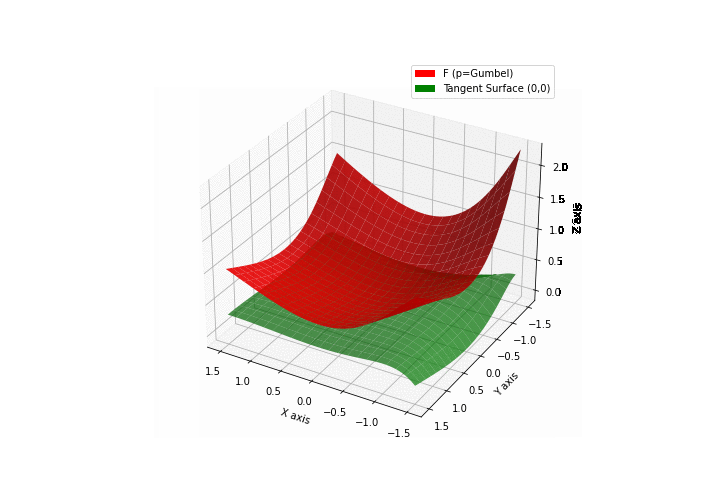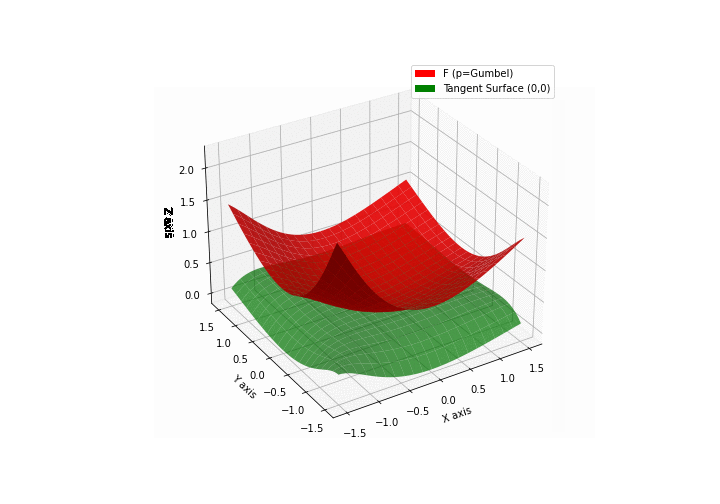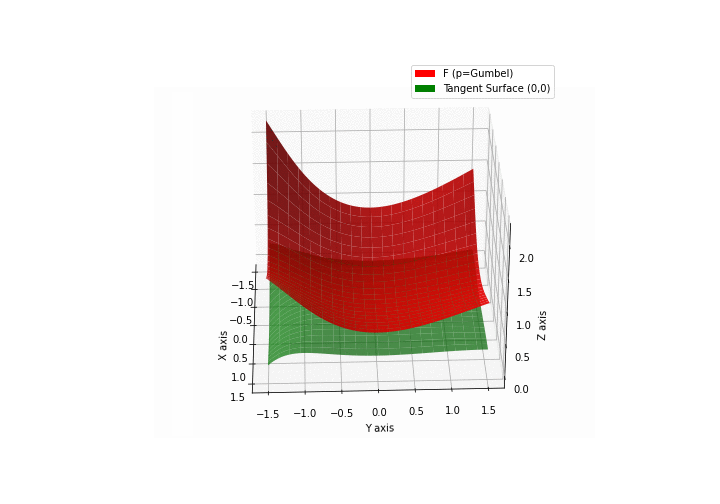
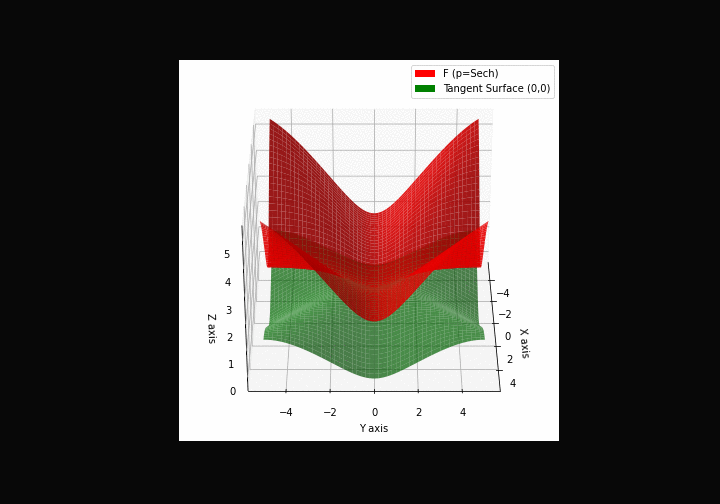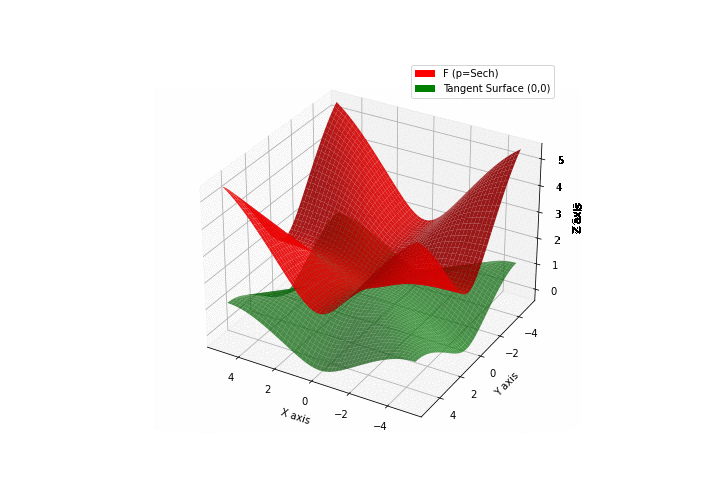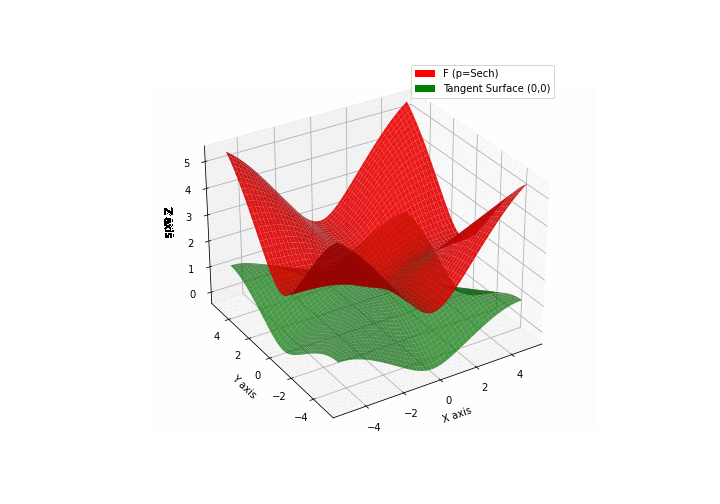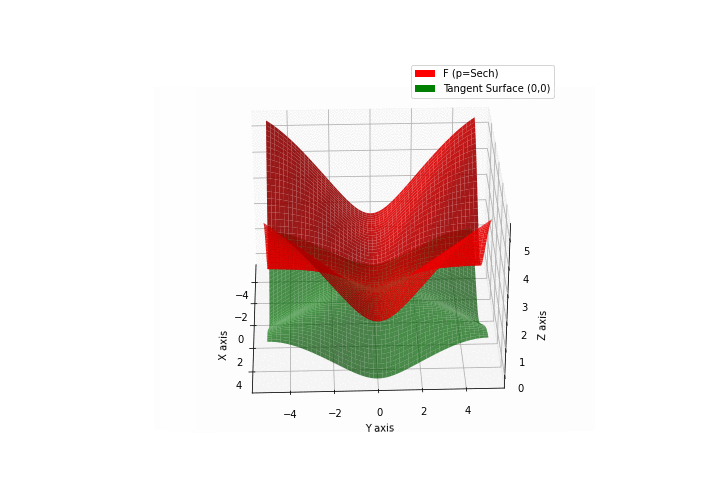
The green tangent surface represents the lower bound in a generalized convexity inequality (see Lemma 1 in “Beyond Log-Concavity: Theory and Algorithm for Sum-Log-Concave Optimization”)
Steps
- Given log-concave function $p$
- Compute cross-convex function $F(x,y)=-\log(p(x)+p(y))$
- Tangent lower bound $\mathcal{T}_{a,b}(x, y) \le F(x,y)$ at point $(a,b)$: \(\mathcal{T}_{a,b}(x, y) = F(a,b) + \nabla F(a,b)^\top \begin{pmatrix} x-a \\ y-b \end{pmatrix} - D_{\text{KL}}\left( \begin{pmatrix} \frac{p(a)}{p(a)+p(b)} \\ \frac{p(b)}{p(a)+p(b)} \end{pmatrix} \, \Bigg \| \, \begin{pmatrix} \frac{p(x)}{p(x)+p(y)} \\ \frac{p(y)}{p(x)+p(y)} \end{pmatrix} \right)\)
- Note: Actually, the negative sign in front of the KL is bad news for the analysis of gradient descent…check out my paper to see how to solve that issue, by considering a reweighted version of the gradient
\(\mathfrak{B}\)estiary
\(\mathcal{G}\)aussian mixture
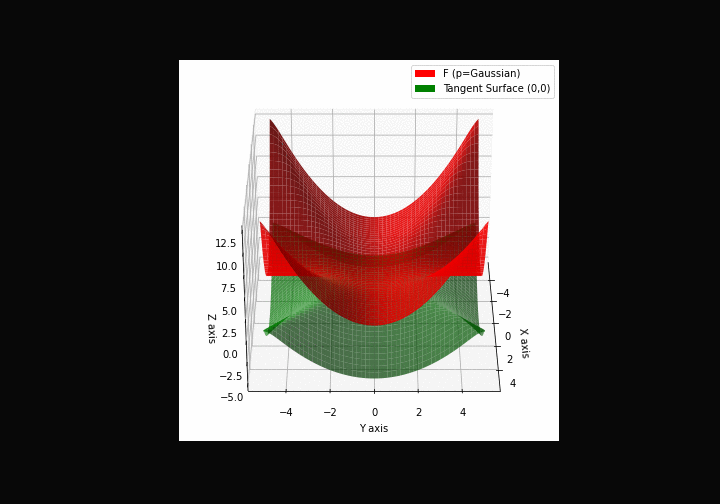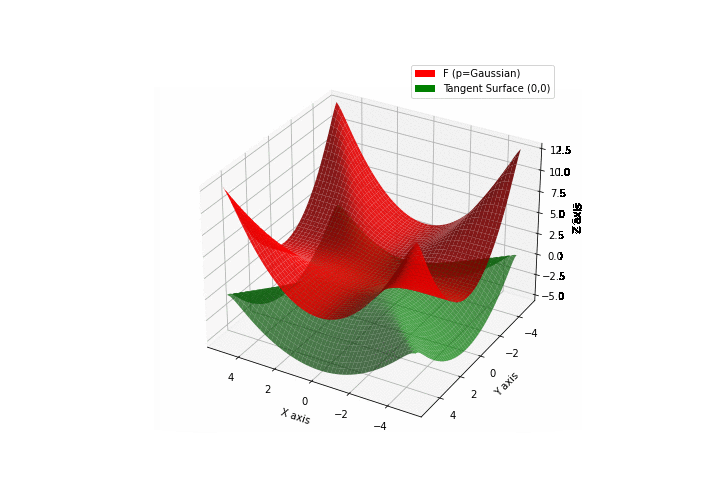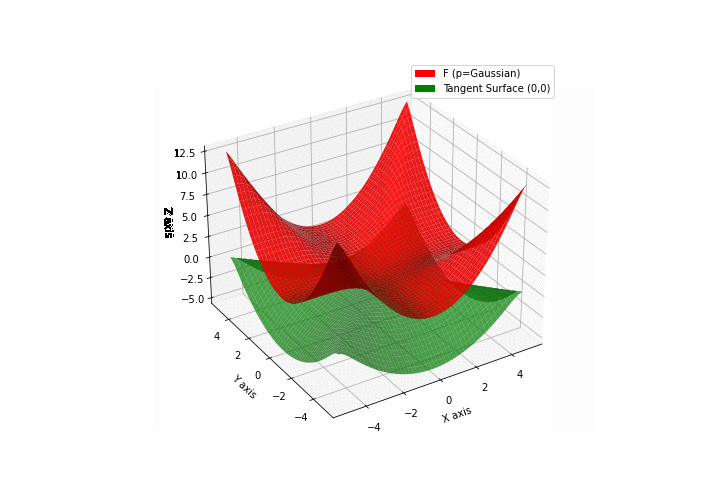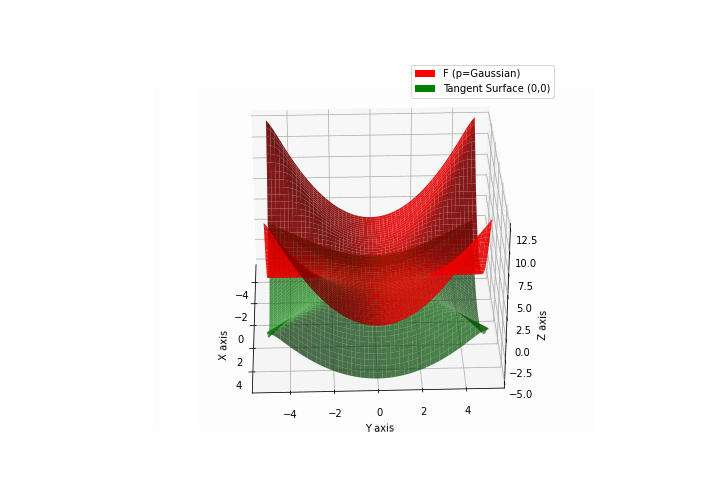
\(\mathcal{L}\)ogistic mixture
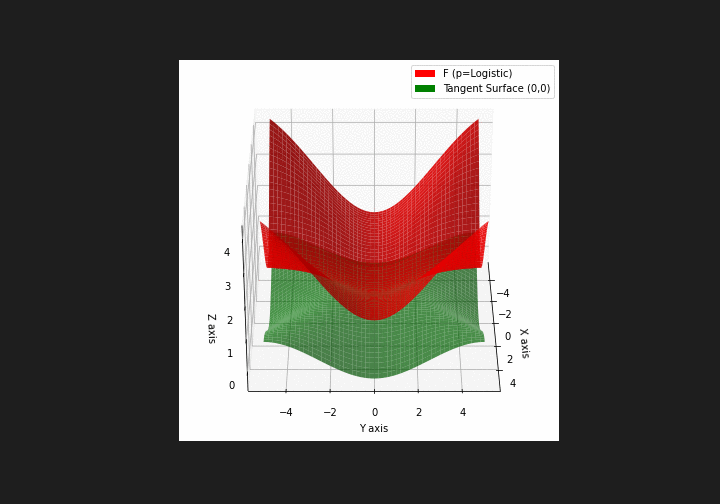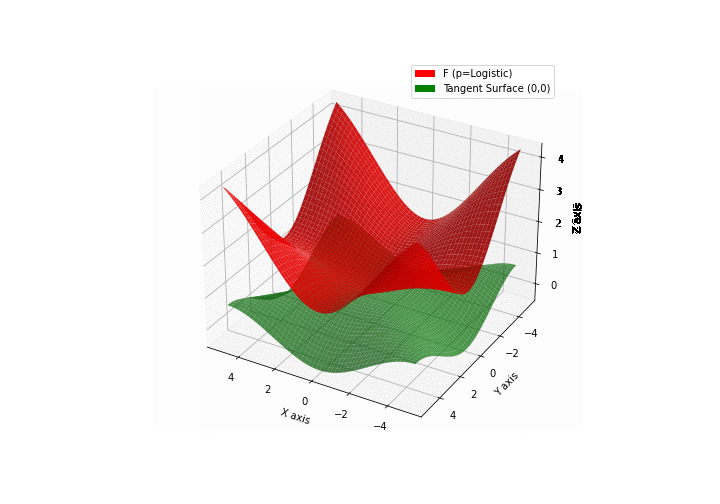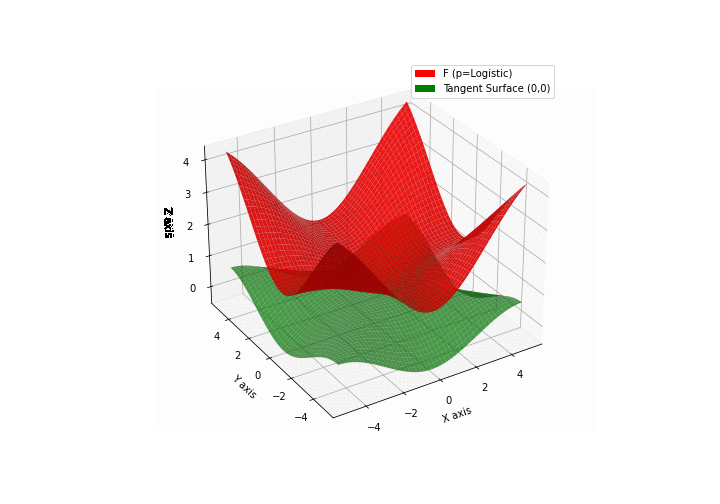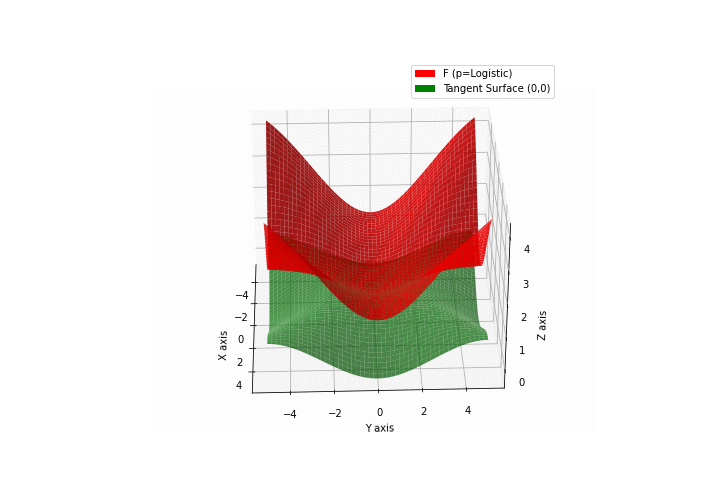
\(\mathcal{H}\)yperbolic \(\mathcal{S}\)ecant mixture
\(\mathcal{G}\)umbel mixture